gamdist

When I was at Tinder, one of my favorite (and most time-consuming) projects was based on Generalized Additive Models. I am pleased to announce that Tinder has agreed to open-source it. I intend to continue developing this project, so expect plenty of posts on this topic as I find time.

I want to thank Dan, Chris, Jeffrey, Tony, Jonathan, Match Legal (esp. Brittany), and Tinder for supporting my work on this project and contributing it to the open-source community.

A Brief Overview

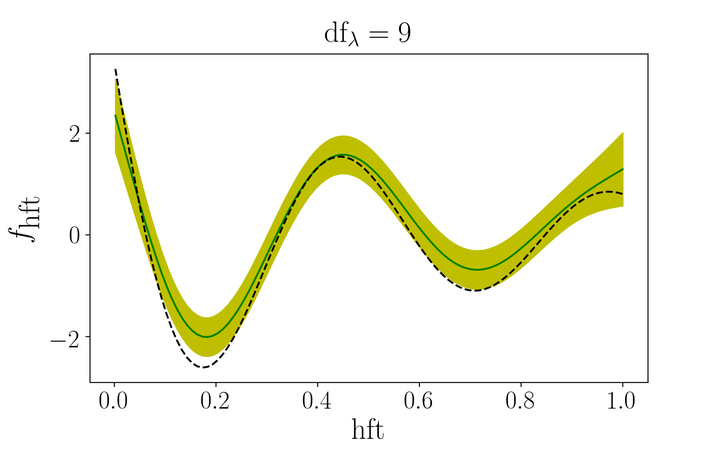
This project started in 2015 when I realized that Python didn’t have any libraries for fitting generalized additive models. ( It does now.) Generalized Additive Models increase the flexibility of Generalized Linear Models (like logistic regression) by removing the assumption of linearity between the features and the transformed response. Perhaps most importantly, this supports modelling non-monotonic relationships between a feature and the response. The image at the top of this page is the result of applying gamdist to a non-monotonic example from “The Elements of Statistical Learning”, by Hastie, Tibshirani, and Friedman.

There is already an R package for doing the same, but because (a) I hate the syntax of R and (b) R is single-threaded,¹ I was inspired to write my own library. The Alternating Direction Method of Multipliers applies quite nicely to fitting additive models in a distributed fashion (the dist in gamdist). I implemented the procedure discussed in [CKB15]; however, I soon learned that getting parallelism working properly in Python is way harder than it should be. I’m embarassed to say I could never really get it working.

Nonetheless, the ADMM architecture led to an unexpected benefit: supporting diverse feature types. Treated as a whole, getting linear, categorical, spline, and piecewise-constant regressors to co-exist makes a holistic approach daunting. Since our approach treats each feature individually², it is easy to mix-and-match different types of features, with radically different regularization methods, while keeping the math pretty clean. In short, ADMM permits applying “separation of concerns” to a statistics problem. I now consider this to be the most compelling reason to use ADMM.

The challenges of the holistic approach lead to clear limitations in existing packages. Suppose I want to apply different amounts of regularization to different features. Scikit-learn can’t do it. Neither can stats-models. (Never mind the fact that neither of these otherwise-commendable packages support generalized additive models.) Suppose I want to apply L1 regularization to one feature, and L2 regularization to another. The standard packages can’t do it.³ Yet when I have applied these techniques in industry, time and time again I have gnashed my teeth at being forced to apply a one-size-fits-all approach to regularization. Our approach makes it trivial to support custom regularization for each feature.

I’ll get off my soapbox for now, especially since I don’t consider this package to be anywhere near complete. (It’s sufficiently complete that I know how to accomplish useful things with it, but I would be impressed if anyone else could get it working.) Nonetheless, open-sourcing it means (a) I can continue to work on it, and (b) anyone can contribute to it. Keep an eye on this site for future announcements.