Interpretable and Validatable Uplift Modeling

1 Introduction
Uplift modeling estimates the impact of a treatment on each individual person, conditional on observed covariates. An individual has a set of observed features, \( X, \) and a pair of potential outcomes, \( (Y(0), Y(1)). \) Uplift modeling estimates \[ \tau(x) := \mathbf{E}[ Y(1) - Y(0) \, | \, X=x]. \] (Gutierrez and Gérardy 2017) offers an introduction to the vast literature on uplift modeling.
Since individual treatment effects are unobservable, it can be difficult to validate an uplift model. Moreover, Machine Learning models like random forests (Wager and Athey 2018) or boosted trees (Powers et al. 2018) are often used, which may hinder intrepretability.
In this paper, we propose a simple method that may be used in addition to existing approaches, to improve interpretability of uplift models. The method also permits validating certain aspects of the resulting predictions. The main contributions of this paper are two novel approaches for adjusting for the multiple comparisons implicit in our proposed method.
In § 2, we discuss an easy-to-understand approach for communicating uplift modeling results. In § 3 we discuss multiplicity adjustments, including two new methods appropriate for tree-like hierarchies of hypotheses. § 4 discusses adaptively selecting which hypotheses to test, resulting in a more informative uplift model. § 5 presents a simulation study. § 6 concludes.
2 Interpretable Uplift Modeling
Shallow decision trees are often used for interpretable Machine Learning. Given an uplift model which predicts the treatment effects for each individual, we may fit a shallow decision tree on the predictions to summarize the most important aspects of the model.
Although individual treatment effects are unobservable, average treatment effects in a population that has been randomly assigned to different levels of treatment are readily estimated. For a fixed population, the difference in average outcomes between the treated and untreated units is an unbiased estimate of the average treatment effect for that population, provided the assignment mechanism is strongly ignorable (Rosenbaum and Rubin 1983; Imbens and Rubin 2015).
The nodes of a decision tree should not be considered fixed populations, because the structure of the tree was selected based on the data. Instead, data splitting offers a simple alternative (Cox 1975). We split the dataset into training and evaluation sets. We fit all models, including the final decision tree, on the training set. Since the evaluation set was not used to determine the model predictions, or the tree structure, statistical inferences may treat the corresponding populations as fixed. An error metric may be defined by comparing the average estimated uplifts, \( \hat{\tau}(x_i), \) with the estimated average treatment effects in each population implied by the nodes of the decision tree.
We may also wish to test hypotheses regarding the average treatment effects within the sub-populations corresponding to each node, or the difference in effects between sub-populations split at each node of the decision tree. For example, if gender corresponds to the first split in the decision tree, we may wish to test \( H_{0, g}: \tau_g \leq 0 \) vs \( H_{A, g}: \tau_g > 0 \) for each gender \( g. \) Rejecting \( H_{0, g} \) proves—in the Frequentist sense of “prove” (Rubin 2004)—the treatment is beneficial for gender \( g. \) Or we may wish to test \( H_{0, g}^\prime: \tau_{g_1} = \tau_{g_2} \) vs \( H_{A, g}^\prime: \tau_{g_1} \neq \tau_{g_2} \) for distinct genders \( g_1, \, g_2. \) Rejecting \( H_{0, g}^\prime \) proves treatment effects vary across genders.
Testing the hypotheses associated with the different nodes and splits must account for the multiple comparisons made. We typically wish to say something about the number of rejected null hypotheses that were falsely rejected; that is, the number of true hypotheses rejected. Each such rejection is called a Type I error, and the goal of multiplicity adjustments is to control the incidence or frequency of these errors. Two commonly considered error rates are the Familywise Error Rate (FWER) and the False Discovery Rate (FDR). The FWER is the probability of rejecting at least one true hypothesis. The FDR is the expected proportion of rejected hypotheses that were in fact true (Dmitrienko, Tamhane, and Bretz 2009, § 2.2).
Controlling the FDR is appealing for exploratory work featuring a large number of hypotheses, but is inappropriate for confirmatory work. It is a lower standard of evidence than controlling the FWER: “any desired conclusion can be almost surely inferred without inflating the FDR” (Dmitrienko, Tamhane, and Bretz 2009, page 39; Finner and Roters 2001). Yet controlling the FWER is often dismissed by practitioners as impractical because of the ubiquity of the overly-conservative Bonferroni correction, and ignorance of superior methods that still control the FWER. In the next section, we propose two new methods that control the FWER in tree-like hierarchies of hypotheses.
3 Strong Control of the Familywise Error Rate in Tree-Like Hierarchies of Hypotheses
The methods proposed in this section operate on a finite or countable collection of hypotheses, \( H_{0,i}, \, i \in \mathcal{I}, \) arranged in a tree-like hierarchy. The root node of this hierarchy will be called \( H_{0,1}. \) Each hypothesis \( i \) has zero or more children indexed by \( \mathcal{J}_i. \) Other than \( H_{0,1}, \) all hypotheses have exactly one parent hypothesis. In our case, \( H_{0,1} \) might correspond to the average treatment effect in the overall population, or it might correspond to the difference in treatment effects between the sub-populations split at the first node of the decision tree.
We generalize two powerful methods for controlling the FWER to the tree-like structures considered here: the Fixed Sequence Procedure (Maurer 1995), and the Fallback Procedure (Wiens 2003; Wiens and Dmitrienko 2005). The Fixed Sequence Procedure tests a priori ordered hypotheses, one at a time. Each hypothesis is tested at the overall desired FWER. Testing continues until we fail to reject a hypothesis. (For brevity, we henceforth say “retain” rather than “fail to reject”.) The Fallback Procedure assigns a weight, \( w_i, \) to each hypothesis, \( i, \) in an a prior ordered sequence. If we test a hypothesis \( i \) at level \( \alpha_i \) and reject it, we test the next hypothesis, \( i + 1, \) at level \( \alpha_{i+1} := w_{i+1} + \alpha_i; \) otherwise, we test it at level \( \alpha_{i+1} := w_{i+1}. \)
Hierarchical Bonferroni Procedure
In this section, we identify a Bonferroni adjustment for controlling the Familywise Error Rate. We do so to contextualize the performance of the methods discussed in subsequent sections. A Bonferroni adjustment assigns a weight to each hypothesis. Provided the weights sum to no more than \( \alpha, \) the FWER is controlled at level \( \alpha. \) Let \( n_k \) be the number of hypotheses at depth \( k \) of the hierarchy, with the root node occurring at depth 1. For example, \( n_1 = 1, \) \( n_2 = | \mathcal{J}_1 |, \) where \( | \mathcal{J}_1 | \) is the number of elements in \( \mathcal{J}_1 \), and \( n_3 = \sum_{j \in \mathcal{J}_1} | \mathcal{J}_j |. \)
The Hierarchical Bonferroni Procedure tests \( H_{0,1} \) at level \( \alpha / 2. \) It tests the hypotheses at depth \( k \) at level \( 2^{-k} \cdot \alpha / n_k, \) \( k=2, \ldots. \) Since the levels at each depth sum to \( 2^{-k} \cdot \alpha, \) the sum of the levels across the entire hierarchy is \( \sum_k 2^{-k} \cdot \alpha \leq \alpha. \)
The Hierarchical Bonferroni Procedure thus controls the FWER at the desired level, but the power corresponding to hypotheses lower in the hierarchy decreases exponentially. As a special case, consider a hierarchy where each hypothesis has exactly 2 children. Then \( n_k = 2^{k - 1}, \) \( k=1, \ldots, \) and the hypotheses at depth \( k \) are tested at level \( 2^{1-2 \cdot k} \cdot \alpha. \)
Fixed Hierarchy Procedure
As with the Hierarchical Bonferroni Procedure, we have a collection of hypotheses in a tree-like hierarchy. For this method, each hypothesis \( H_{0,i}, \) other than \( H_{0,1}, \) has an associated weight, \( w_i, \) with \( 0 \leq w_i \leq 1 \), and \( \sum_{j \in \mathcal{J}_i} w_j = 1 \) for all \( i. \)
The Fixed Hierarchy Procedure tests \( H_{0,1} \) at level \( \alpha_1 = \alpha. \) If we retain \( H_{0,1}, \) testing stops; otherwise, we test each child at level \( w_j \cdot \alpha, \) \( j \in \mathcal{J}_1. \) Progressing down the tree, if we test \( H_{0,i} \) at level \( \alpha_i, \) and retain \( H_{0,i}, \) we do not test any descendants of \( H_{0,i}. \) Otherwise, we test each child of \( H_{0,i} \) at level \( w_j \cdot \alpha_i, \) \( j \in \mathcal{J}_i. \) Remark: the Fixed Sequence Procedure is a special case of the Fixed Hierarchy Procedure, where each hypothesis has at most one child.
Proposition: The probability the Fixed Hierarchy Procedure rejects at least one true hypothesis is at most \( \alpha. \)
Proof: The proof is by induction on the depth of the tree. Let \( A \) be the event that a Type I error has occurred. Let \( B_i \) be the event that \( H_{0,i} \) is rejected. If none of the hypotheses are true, there is no possibility of falsely rejecting a true hypothesis, so \( \mathrm{Pr}\{ A \} = 0. \) Thus, throughout we assume at least one hypothesis is true.
The proof makes repeated use of the fact that if \( j \in \mathcal{J}_i \) and \( H_{0,j} \) is true, then \( \mathrm{Pr}\left\{ B_j \, \middle| \, B_i \right\} \leq w_j \cdot \alpha_i \) since \( B_j \) is tested at level \( w_j \cdot \alpha_i. \) If \( H_{0,j} \) is false, all we can say is that \( \mathrm{Pr}\left\{ B_j \, \middle| \, B_i \right\} \leq 1. \)
For the basis step, consider a tree of depth 2. Suppose \( H_{0,1} \) is true. Then
\begin{align*} \mathrm{Pr}\{ A \} &= \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \\ &= 1 \cdot \mathrm{Pr}\left\{ B_1 \right\} + 0 \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \\ &= \mathrm{Pr}\left\{ B_1 \right\} \\ &\leq \alpha, \end{align*}
since \( H_{0,i} \) is tested at level \( \alpha. \) The key idea is that if we retain \( H_{0,1}, \) we do not test any other hypotheses, and so there is no possibility of rejecting a true hypothesis in that case.
Now suppose \( H_{0,1} \) is false. Then at least one child of \( H_{0,1} \) must be true. Let \( J^\prime \subseteq \mathcal{J}_i \) denote the indices corresponding to true hypotheses.
\begin{align*} \mathrm{Pr}\{ A \} &= \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \\ &\leq \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \\ &= \mathrm{Pr}\left\{ \cup_{j \in J^\prime} B_j \, \middle| \, B_1 \right\} \\ &\leq \sum_{j \in J^\prime} \mathrm{Pr}\left\{ B_j \, \middle| \, B_1 \right\} \\ &\leq \sum_{j \in J^\prime} w_j \cdot \alpha \\ &\leq \alpha, \end{align*}
where the fourth line applied Boole’s inequality. That concludes the basis step.
Now suppose the Fixed Hierarchy Procedure controls the FWER at the specified level for trees of depth up to \( N. \) Consider a tree of depth \( N + 1. \) The same argument from the basis step shows that if \( H_{0,1} \) is true, then \( \mathrm{Pr}\left\{ A \right\} \leq \alpha. \) Suppose \( H_{0,1} \) is false. Let \( K_i \) denote the set of hypotheses consisting of \( H_{0,i} \) and all of its descendants. Let \( A_i \) be the event that a Type I error is made among the hypotheses in \( K_i. \)
\begin{align*} \mathrm{Pr}\left\{ A \right\} &\leq \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \\ &= \mathrm{Pr}\left\{ \cup_{j \in \mathcal{J}_1} A_j \, \middle| \, B_1 \right\} \\ &\leq \sum_{j \in \mathcal{J}_1} \mathrm{Pr}\left\{ A_j \, \middle| \, B_1 \right\} \\ &\leq \sum_{j \in \mathcal{J}_1} w_j \cdot \alpha = \alpha. \end{align*}
The second line observes that if a Type I error is made, it must be among at least one of the children of \( H_{0,1}, \) or a descendant. The last line uses the inductive hypothesis. Since \( K_j \) is a tree of depth at most \( N, \) the FWER is controlled at the stated level.
To compare the performance of the Fixed Hierarchy Procedure with that of the Hierarchical Bonferroni Procedure, consider a hierarchy where each hypothesis has exactly 2 children, and \( w_i = 1/2 \) for all \( i. \) Assuming all ancestors are rejected, the Fixed Hierarchy Procedure tests a hypothesis at depth \( k \) at level \( 2^{1 - k} \cdot \alpha, \) compared to \( 2^{1 - 2 \cdot k} \cdot \alpha \) for the Hierarchical Bonferroni Procedure. Thus, the Fixed Hierarchy Procedure potentially represents an exponential improvement over the Bonferroni adjustment. Table 1 shows how quickly the level at which hypotheses are tested falls off as we get deeper in the hierarchy, when using the two procedures.
| Depth | Bonferroni | Fixed Hierachy |
|---|---|---|
| 1 | \( \alpha/2 \) | \( \alpha \) |
| 2 | \( \alpha/8 \) | \( \alpha / 2 \) |
| 3 | \( \alpha/32 \) | \( \alpha / 4 \) |
| 4 | \( \alpha/128 \) | \( \alpha / 8 \) |
Assuming hypotheses early in the hierarchy are tested with high power, the advantage over the Bonferroni adjustment is clear. The increased power comes at the cost of decreased flexibility, however; failing to reject the first hypothesis means the Fixed Hierarchy Procedure fails to reject any hypotheses, even if those hypotheses would be rejected by the Bonferroni adjustment. The method proposed in the next section addresses this by allowing testing to continue even when a hypothesis is retained, but at lower power.
Trickle Down Procedure
As before, each hypothesis has a weight, \( w_i. \) Each hypothesis now also has a stake, \( 0 < v_i \leq 1. \) The name is intended in the sense of a wager: something risked. We also introduce the notion of the available level, connected to the level at which a hypothesis is tested, by the corresponding stake. If \( H_{0,i} \) has available level \( \alpha_i, \) it will be tested at level \( v_i \cdot \alpha_i. \)
The Trickle Down Procedure assigns \( H_{0,1} \) to have available level \( \alpha_1 := \alpha, \) testing it at level \( v_1 \cdot \alpha. \) The available level of hypotheses farther down in the hierarchy depends on which hypotheses farther up in the hierarchy were rejected. Suppose \( H_{0,i} \) has available level \( \alpha_i \) (and is thus tested at level \( v_i \cdot \alpha_i\) ). Each child is assigned an available level depending on whether the parent was rejected: \[ \alpha_j := \begin{cases} w_j \cdot \alpha_i & H_{0,i} \textrm{ rejected} \\ w_j \cdot (1 - v_i ) \cdot \alpha_i & H_{0,i} \textrm{ retained}, \end{cases} \] \( j \in \mathcal{J}_i. \)
The intuition is that when \( H_{0,i} \) is tested, we wager only a portion, \( v_i, \) of the available level, \( \alpha_i, \) testing \( H_{0,i} \) at level \( v_i \cdot \alpha_i. \) If we reject \( H_{0,i}, \) the entire available level, \( \alpha_i, \) is split among the children. If we fail to reject \( H_{0,i}, \) the stake is forfeit, but the unwagered portion, \( (1 - v_i) \cdot \alpha_i, \) is still available for continued testing. Remark: the Fixed Hierarchy Procedure is a special case of the Trickle Down Procedure, where \( v_i = 1 \) for all \( i. \) That is, the Fixed Hierarchy Procedure stakes the entire available level at each opportunity. The Fallback Procedure is analogous to the Trickle Down Procedure when each hypothesis has at most one child, but with different weights.
*Proposition: * The probability the Trickle Down Procedure rejects at least one true hypothesis is at most \( \alpha. \)
Proof: The proof is conceptually identical to the proof for the Fixed Hierarchy Procedure, but somewhat more tedious since retaining a hypothesis still permits subsequent Type I errors. As before, if all hypotheses are false, there is no possibility of a Type I error, so assume at least one hypothesis is true.
For the basis step, consider a tree of depth 2. Suppose \( H_{0,1} \) is true. Let \( \mathcal{J}^\prime \subseteq \mathcal{J}_1 \) denote the (possibly empty) true hypotheses in \( \mathcal{J}_1. \) Then
\begin{align} \mathrm{Pr}\left\{ A \right\} &= \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \nonumber \\ &= 1 \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \nonumber \\ &= \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ \cup_{j \in J^\prime} B_j \, \middle| \, \neg B_1 \right\} \cdot \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot \sum_{j \in J^\prime} \mathrm{Pr}\left\{ B_j \, \middle| \, \neg B_1 \right\} \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot \sum_{j \in J^\prime} v_j \cdot w_j \cdot (1 - v_1) \cdot \alpha \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \label{eqn:basis} \\ &= (1 - v_1) \cdot \alpha + \mathrm{Pr}\left\{ B_1 \right\} \cdot (1 - (1 - v_1) \cdot \alpha) \nonumber \\ &\leq (1 - v_1) \cdot \alpha + v_1 \cdot \alpha \cdot (1 - (1 - v_1) \cdot \alpha) \nonumber \\ &= \alpha - v_1 \cdot (1 - v_1) \cdot \alpha^2 \nonumber \\ &\leq \alpha. \nonumber \end{align}
Now suppose \( H_{0,1} \) is false. We have
\begin{align} \mathrm{Pr}\left\{ A \right\} &= \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} \cdot \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \nonumber \\ &= \mathrm{Pr}\left\{ B_1 \right\} \cdot \mathrm{Pr}\left\{ \cup_{j \in J^\prime} B_j \, \middle| \, B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} \cdot \sum_{j \in J^\prime} \mathrm{Pr}\left\{ B_j \, \middle| \, B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} \cdot \sum_{j \in J^\prime} v_j \cdot w_j \cdot \alpha + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \nonumber \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} \cdot \alpha + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \label{eqn:basis2} \\ &= (1 - v_1) \cdot \alpha + \mathrm{Pr}\left\{ B_1 \right\} \cdot v_1 \cdot \alpha \nonumber \\ &\leq \alpha, \nonumber \end{align}
where the second line recycles the inequality regarding \( \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \) from the previous case. This completes the basis step.
Now assume the Trickle Down Procedure controls the FWER for hierarchies of depth up to \( N. \) Consider a tree of depth \( N + 1. \) Suppose \( H_{0,1} \) is true. Then
\begin{align*} \mathrm{Pr}\left\{ A \right\} &= \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \\ &= \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ \cup_{j \in \mathcal{J}_1} A_j \, \middle| \, \neg B_1 \right\} \cdot \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot \sum_{j \in \mathcal{J}_1} \mathrm{Pr}\left\{ A_j \, \middle| \, \neg B_1 \right\} \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot \sum_{j \in \mathcal{J}_1} w_j \cdot (1 - v_1) \cdot \alpha \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \\ &\leq \alpha. \end{align*}
The fourth line follows from the inductive hypothesis. Since \( K_j \) is a hierarchy of depth no more than \( N, \) the procedure controls the FWER at the specified level. Unlike with the Fixed Hierarchy Method, the overall level, \( w_j \cdot (1 - v_1) \cdot \alpha, \) is distinct from the level at which \( H_{0,j} \) is tested, \( v_j \cdot w_j \cdot (1 - v_1) \cdot \alpha. \) The penultimate line equals (\ref{eqn:basis}), so the remaining inequality is the same.
Now suppose \( H_{0,1} \) is false. We have
\begin{align*} \mathrm{Pr}\left\{ A \right\} &= \mathrm{Pr}\left\{ A \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ A \, \middle| \, \neg B_1 \right\} \cdot \mathrm{Pr}\left\{ \neg B_1 \right\} \\ &= \mathrm{Pr}\left\{ \cup_{j \in \mathcal{J}_1} A_j \, \middle| \, B_1 \right\} \cdot \mathrm{Pr}\left\{ B_1 \right\} + \mathrm{Pr}\left\{ \cup_{j \in \mathcal{J}_1} A_j \, \middle| \, \neg B_1 \right\} \cdot \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} \cdot \sum_{j \in \mathcal{J}_1} \mathrm{Pr}\left\{ A_j \, \middle| \, B_1 \right\} + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot \sum_{j \in \mathcal{J}_1} \mathrm{Pr}\left\{ A_j \, \middle| \, \neg B_1 \right\} \\ &\leq \mathrm{Pr}\left\{ B_1 \right\} \cdot \sum_{j \in \mathcal{J}_1} w_j \cdot \alpha + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot \sum_{j \in \mathcal{J}_1} w_j \cdot (1 - v_1) \cdot \alpha \\ &= \mathrm{Pr}\left\{ B_1 \right\} \cdot \alpha + \left( 1 - \mathrm{Pr}\left\{ B_1 \right\} \right) \cdot (1 - v_1) \cdot \alpha \\ &\leq \alpha, \end{align*}
where the penultimate line equals (\ref{eqn:basis2}).
The Trickle Down Procedure provides more flexibility than the Fixed Hierarchy Procedure, while offering potentially more power than a Bonferroni adjustment. To see this, suppose each hypthesis has exactly two children, and let \( w_i = v_i = 1/2 \) for all \( i. \) The level at which hypotheses, other than the root hypothesis, are tested, depends on whether previous hypotheses were rejected.
Consider then two possibilities: first that all hypotheses have been rejected, second that all hypotheses are retained. Table 2 shows the level at which a hypothesis at a particular depth is tested. When all hypotheses are retained, the Trickle Down Procedure is no better (and no worse) than the Bonferroni adjustment. But when hypotheses are rejected, subsequent hypotheses are tested at higher levels than with Bonferroni. The Trickle Down Procedure has power no worse, and potentially exponentially better than, Bonferroni.
| Depth | Bonferroni | Trickle Down | Trickle Down | Fixed Hierarchy |
|---|---|---|---|---|
| (all retained) | (all rejected) | |||
| 1 | \( \alpha/2 \) | \( \alpha/2 \) | \( \alpha/2 \) | \( \alpha \) |
| 2 | \( \alpha/8 \) | \( \alpha/8 \) | \( \alpha/4 \) | \( \alpha/2 \) |
| 3 | \( \alpha/32 \) | \( \alpha/32 \) | \( \alpha/8 \) | \( \alpha/4 \) |
| 4 | \( \alpha/128 \) | \( \alpha/128 \) | \( \alpha/16 \) | \( \alpha/8 \) |
Connection to Gatekeeping Procedures
Gatekeeping procedures are popular in the planning and analysis of clinical trials (Dmitrienko, Tamhane, and Bretz 2009, § 5). Gatekeeping procedures exist for testing tree-like hierarchies of hypotheses (Dmitrienko and Tamhane 2011), yet the method proposed in this paper appears to be new.
4 Adaptively Selecting Hypotheses
Data splitting not only permits inferences after model training. It also gives us some flexibility in adapting the hypotheses tested to the data at hand. Let \( H_{0,i}^+(\delta_i): \tau_i \leq \delta_i, \) where \( \tau_i \) is the average treatment effect in the population, \( \mathcal{P}_i, \) corresponding to node \( i, \) and \( \delta_i \) is some suitable value allowed to vary by population. For example, rejecting \( H_{0,i}^+(0) \) proves the treatment is beneficial, on average, for population \( \mathcal{P}_i. \)
Setting \( \delta_i \) to be some small negative quantity implements a non-inferiority test, while setting \( \delta_i \) to be some meaningful positive quantity implements a superiority test. Non-inferiority tests are sometimes used in product analytics, where an important new feature will be released unless it actively harms some key business metric. Superiority tests are useful anytime administering the treatment comes at a cost, such as offering a discount, or spending marketing dollars. In such a case, we need to know the benefit to the metric outweighs the cost. We would set \( \delta_i \) to represent this break-even point.
If we wanted to reject every single hypothesis in the family \( \{ H_{0,i}^+(\delta_i) \}_{i \in \mathcal{I}}, \) one attractive option is to test each hypothesis at level \( \alpha. \) By the Intersection-Union principle (Berger 1982), this controls the FWER at level \( \alpha. \) Even if the treatment is beneficial in each subpopulation, we may not have enough power to reject it in each subpopulation. This is especially likely in deep trees with modest sample sizes. Worse, failing to reject even a single hypothesis prevents us from certifying the treatment as beneficial in any population.
The Fixed Hierarchy and Trickle Down Procedures offer attractive alternatives. Assuming the treatment is indeed beneficial, we would have maximal power in the top nodes to validate the treatment. Failure to reject hypotheses deeper in the tree correspond to smaller populations of less business significance.
Failing to reject \( H_{0,i}^+(\delta_i) \) does not prove the treatment was harmful in \( \mathcal{P}_i \)—it doesn’t prove anything (Rosenbaum 2019, page 44). We may fail to reject a hypothesis in a node corresponding with a large or otherwise important population, leaving us in a state of unacceptable uncertainty. Because we already split the data into training and evaluation sets, we can do better.
Let \( H_{0, i}^-(\delta_i) : \tau_i \geq \delta_i. \) Rejecting \( H_{0, i}^-(\delta_i) \) proves the treatment is harmful in the sense implied by \( \delta_i. \) For example when \( \delta_i \) is the break-even threshold for an expensive treatment, rejecting \( H_{0, i}^-(\delta_i) \) proves the benefit did not justify the cost in population \( \mathcal{P}_i. \)
When we train our uplift model and fit a decision tree to the resulting treatment effect estimates, we can also use the training set to decide which hypotheses to test: \( H_{0,i}^+ \) or \( H_{0,i}^-. \) We can calculate average treatment effects, \( \hat{\tau}_{i, \textrm{train}}, \) where the notation makes it explicit this estimate is based on the training set. If \( \hat{\tau}_{i,\textrm{train}} > \delta_i, \) we would select \( H_{0,i}^+(\delta_i) \) for testing in the evaluation set. Otherwise we would select \( H_{0,i}^-(\delta_i). \) Rejecting the selected hypothesis in node \( i \) certifies what we informally observe in the training set.
There are two advantages to this adaptive approach. First, we are likely to reject more hypotheses, increasing the power available to lower nodes in the decision tree. It also reduces the uncertainty at the end of the analysis: if a treatment really is harmful in some subpopulations, the approach is able to certify it as such.
In principle, we could even choose \( \delta_i \) adaptively by performing power analysis in each node and setting \( \delta_i \) to be the largest (or smallest) value still leading us to have sufficient power to reject \( H_0^+ \) (or \( H_0^- \)). Note that power is deflated in multiple testing scenarios, and further research is needed for power analysis in this setting.
Let \( H_{0,i}^\prime \) be the hypothesis selected during training for testing using the evaluation set. Since these hypotheses were chosen without reference to the evaluation set, testing them using the Fixed Hierarchy or Trickle Down Procedures controls the FWER.
It’s also possible to test for heterogeneous treatment effects while also testing for their signs or magnitudes. We do this by interweaving \( H_{0, i} \) and \( H_{0, i}^\prime. \) Each treatment effect hypothesis \( H_{0, i}^\prime \) has exactly one child, \( H_{0, i}, \) and each heterogeneity hypothesis \( H_{0, i} \) has children \( H_{0, j}^\prime, \) \( j \in \mathcal{J}_i. \) In words, we first test the magnitude of the treatment effect in a node, and then test whether treatment effects are heterogeneous across the children of that node. If so, we would then test the magnitude of the treatment effects in those child nodes, exploring as much of the tree as the procedures allow.
5 Simulation Study
To illustrate the method, both the construction of a decision tree and the resulting insights, we conducted a simulation study.
First we generated 10 features at random, for 10,000 individuals. The features were a mix of binary, continuous, and categorical variables of various cardinalities. Next we simulated potential outcomes for each individual as a function of the features, plus random noise. We randomly assigned each individual to either treatment or control, and recorded the corresponding potential outcome as the observed outcome. We deleted the underlying potential outcomes to mimic what we observe in reality: some features, a treatment indicator, and the observed outcome.
Next we randomly split the 10,000 individuals approximately in half, into training and evaluation datasets. We fit a T-learner uplift model on the training set, using XGBoost (Chen and Guestrin 2016) as the base learner. Specifically, we fit a model, \( \hat{\mu}_0, \) on the training individuals having \( z = 0 \), and did the same for \( z = 1, \) resulting in \( \hat{\mu}_1. \) The treatment effect was estimated as \( \hat{\mu}_1(x) - y_\textrm{obs} \) or \( y_\textrm{obs} - \hat{\mu}_0(x) \) for each individual in the control or treatment group, resp.
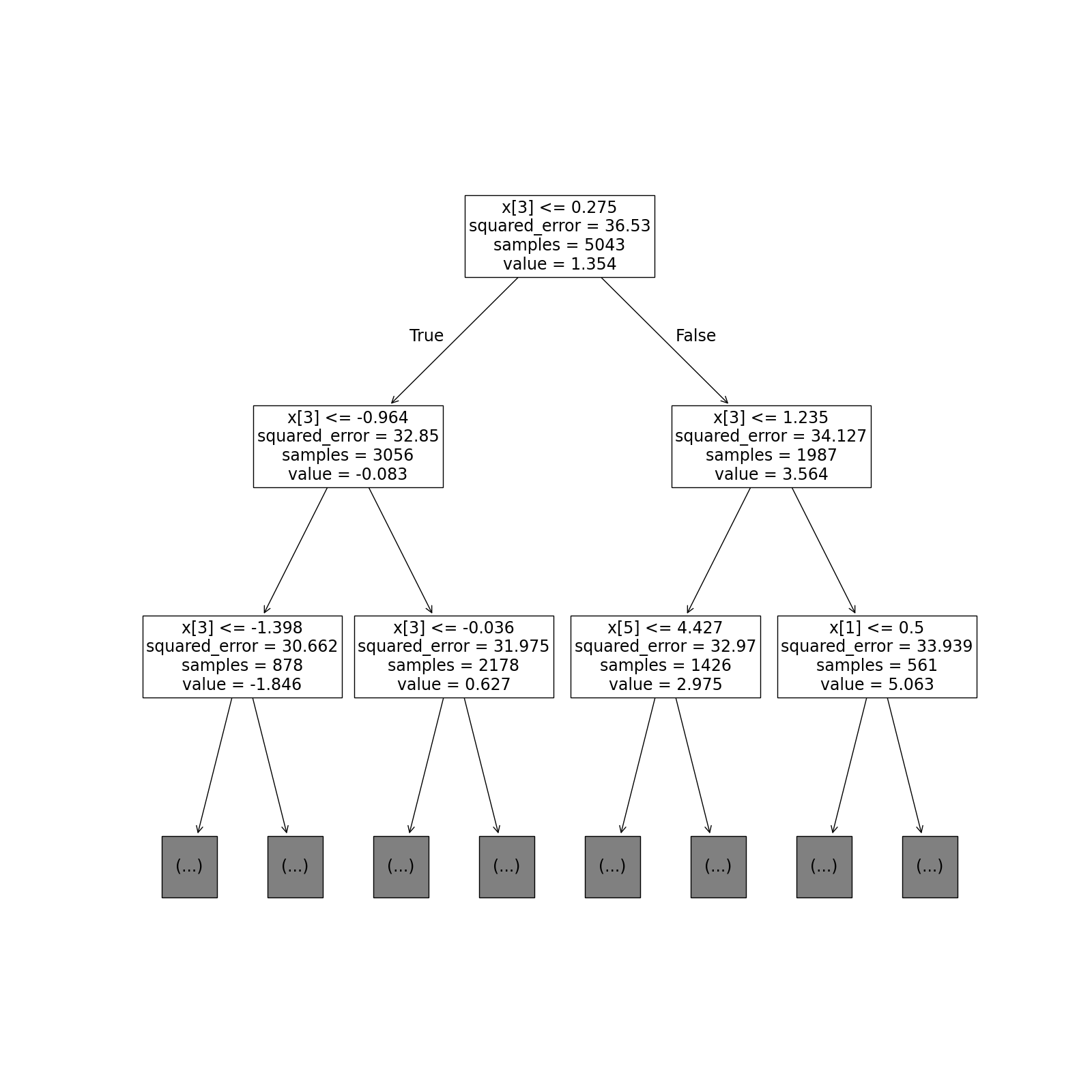
Next we fit a decision tree on the estimated treatment effects (in the training dataset). The results are shown in Figure 1. While the tree was allowed to be quite deep, only the first few levels are shown.
6 Summary
We have presented an intuitive yet rigorous approach to presenting the results of an uplift model. The key contributions of this paper are the development of two approaches for controlling the Familywise Error Rates in tree-like hierarchies of hypotheses. The Fixed Hierarchy Procedure generalizes the Fixed Sequence Procedure, and the Trickle Down Procedure generalizes the Fallback Procedure. The Trickle Down Procedure offers the flexibility of a Bonferroni adjustment, with exponentially better power as more hypotheses are rejected.