Minimum Edit Distance

Recently I’ve been working on the Natural Language Processing specialization from deeplearning.ai. I wasn’t completely clear on the explanation of minimum edit distance, so I decided to write it out.

Minimum Edit Distance is defined as the minimum number of edits needed to transform a source string to a target string, using edits:

• Delete a character
• Insert a character
• Replace a character

Each type of edit has an associated cost, and we seek a sequence of edits having minimal cost.

Given:

• $d$: cost of deleting a character
• $i$: cost of inserting a character
• $r$: cost of replacing a character
• source: source string, having length $m$
• target: target string, having length $n$

Return: A sequence of edits that transform source into target with minimal cost. Notably, this sequence is not necessarily unique, but out of all edit sequences transforming source into target, there should not exist a sequence having lower cost than that associated with the edit sequence returned by this algorithm.

Define:

• $s_i$: the first $i$ characters of source, for $i=0,\ldots,m$ ($s_0$ is the empty string and $s_m$ is source itself.)
• $t_j$: the first $j$ characters of target, for $j=0,\ldots,n.$
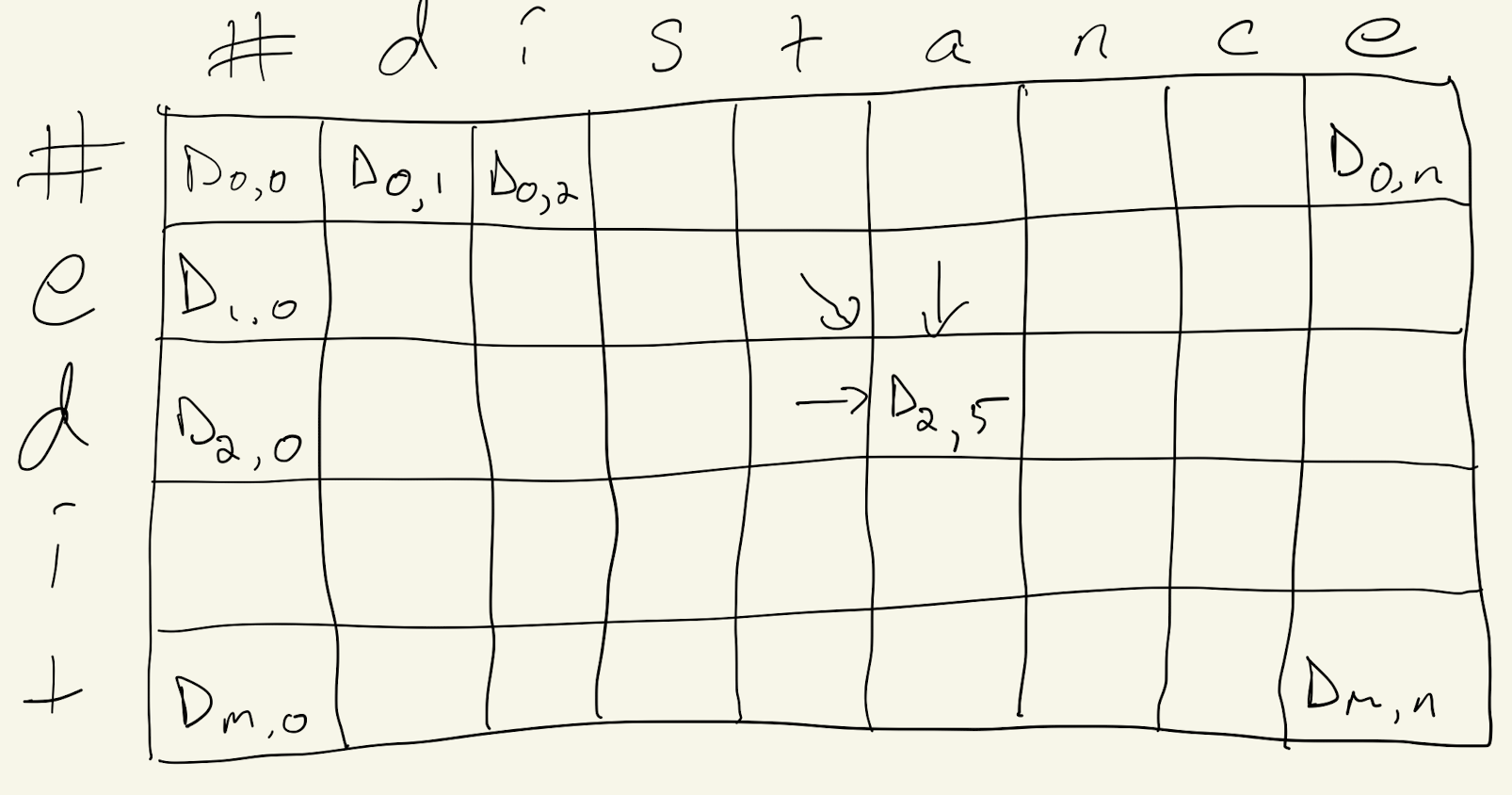
• $D_{i,j}$: minimum edit distance from $s_i$ to $t_j,$ for $i=0,\ldots,m$ and $j=0,\ldots,n.$

The algorithm uses dynamic programming both to calculate the minimum edit distance and to identify a corresponding sequence of edits. Notably, the minimum edit distance from source to target is $D_{m,n},$ but it is not immediately obvious how to calculate that. Instead, we focus on quantities $D_{i,j}$ that are obvious how to calculate and build up to the answer.

Starting with $D_{0,0},$ the minimum edit distance from the empty string to the empty string, we see that this is zero since there are no edits required. Moving on to $D_{1,0},$ the distance from the first character of source to the empty string, we see that this is simply the delete cost $d$ since we merely need to delete a single character. Similarly, $D_{i,0}$ is $i$ times the delete cost since we just need to delete $i$ characters.

Next, we see that $D_{0,1},$ the distance from the empty string to the first character of target, is the cost of inserting a single character. Similarly, $D_{0,j}$ is $j$ times the insert cost since we insert $j$ characters.

So far we have identified quantities $D_{i,j}$ that could be calculated by inspection (which is a mathematically nice way of saying “hand-wavy argument”). Next let’s consider $D_{i,j},$ the minimum edit distance from $s_i$ to $t_j.$ There are three ways of transforming $s_i$ to $t_j.$

First, we could delete the last character of $s_i,$ yielding $s_{i-1},$ and then transform $s_{i-1}$ to $t_j$ (somehow). The cost of this composite transformation is the cost of deleting a character plus the cost of transforming from $s_{i-1}$ to $t_j,$ which is $d + D_{i-1,j}.$ Second, we could transform $s_i$ to $t_{j-1}$ and then insert the final character of $t_j.$ The cost here is $D_{i,j-1} + i.$ Finally, we could neglect the final characters of $s_i$ and $t_j$ and transform $s_{i-1}$ to $t_{j-1},$ and then replace the last character of $s_i$ with the last character of $t_j.$ Of course, if the last character of $s_i$ is the same as the last character of $t_j$ then there is no need to replace anything. This then either has cost $D_{i-1,j-1} $ or $D_{i-1,j-1} + r$ depending on whether the last characters are the same or not. The minimum edit distance is the minimum over these three possibilities:

$$ D_{i,j} = \min \begin{cases} d + D_{i-1,j} \\ D_{i,j-1} + i \\ D_{i-1,j-1} + r \cdot I\{\textrm{last characters differ}\}. \end{cases} $$

We see that calculating $D_{i,j}$ is easy, provided we already know $D_{i-1,j},$ $D_{i,j-1}$ and $D_{i-1,j-1}.$ In Figure 1, we have arranged the $D_{i,j}$ values in a table, with $D_{0,0}$ in the top left corner and $D_{m,n}$ in the bottom right. To calculate an entry (other than first row or first column), we need the entries to the left, above, and diagonally left and up, as denoted by the arrows. Provided we populate each element, starting with the first row, and going left to right, by the time we need to calculate a particular entry, we already will have calculated everything we need. Since we calculate each entry in the table, the algorithm runs in $\mathcal{O}(mn)$ time and uses the same amount of space.

Getting the sequence of edits is comparatively straightforward but requires some additional notation. Let $E_{i,j}$ be the minimal cost sequence of edits transforming $s_i$ to $t_j.$ We denote a single edit with a notational element like $e.$ A sequence of edits is denoted as the composition of multiple edits, like $e_2 \circ e_1,$ which should be interpreted as applying $e_1$ and then $e_2$ (reading right to left). The application of a particular sequence of edits to a given string is denoted by $E_{i,j}(source)$ or $(e_2 \circ e_1)(source).$ We will restrict edits to:

• Deleting the last character of a string, denoted $e_d.$
• Inserting the last character of a given string onto the end of another string, denoted $e_i(t_j).$ For example, $(e_i(\textrm{dogs}))(\textrm{cat})=\textrm{cats},$ since we take the last character of dogs, s, and insert it at the end of cat to produce cats.
• Replacing the last character of one string with the last character of another string, denoted $e_r(t_j).$ For example, $(e_r(\textrm{bar}))(\textrm{cat})=\textrm{car},$ since we replace the last character of cat, t, with the last character of bar, r, to produce car.

We also require the ability to restrict a sequence of edits to the first $k$ characters of a string, without affecting the remainder. We denote this with a superscript, so $E^k$ applies a sequence of zero or more edits to the first $k$ characters of a string. We can imagine it sets the remaining characters aside, performs the transformation, then puts the characters back at the end. This is a little messy but is unfortunately needed for handling replacements. If we think of a replace as being a delete followed by an insert, the notation is a little cleaner, as we will see.

Following a similar sequence of logic that led us to $D_{i,j},$ we start with $E_{0,0},$ which does not require any edits, so $E_{0,0}$ is simply the identity transformation, $I.$ Next, $E_{1, 0}$ is clearly just $e_d$ since we simply need to delete a character. Similarly, $E_{i,0}$ is just $e_d \circ \cdots \circ e_d$ with the composition of $i$ entries $e_d.$ Next, $E_{0,1}$ is $e_i(t_1),$ since we simply insert the character we need. Similarly, $E_{0,j}$ is $e_i(t_j) \circ e_i(t_{j-1}) \circ \cdots \circ e_i(t_1),$ keeping in mind that this is read right-to-left: first we insert the first character, then the second, and so forth.

Just as $D_{i,j}$ is compute in terms of $D_{i-1,j},$ $D_{i, j-1},$ and $D_{i-1,j-1},$ so too is $E_{i,j}$ computed in terms of other sequences. Specifically, $E_{i, j}$ corresponds to one of the three following possibilities:

• Delete a character from the end of $s_i,$ and then transform from $s_{i-1}$ to $t_j.$ This is denoted by $E_{i-1, j} \circ e_d$ (recall that we read right-to-left).
• Transform from $s_i$ to $t_{j-1}$ and then insert the last character of $t_j.$ This is denoted by $e_i(t_j) \circ E_{i, j-1}.$
• Transform all but the last character of $s_i$ to all but the last character of $t_j,$ then replace the last character of $s_i$ with the last character of $t_j,$ denoted by $e_r(t_j) \circ E_{i-1, j-1}^{i-1}.$ As before, if the last character of $s_i$ is the same as the last character of $t_j,$ there is no need to do the replace step, so the transformation here is simply $E_{i-1,j-1}^{i-1}.$ We see now why we needed that annoying superscript notation, so the idea of transforming all but the last character is notationally possible. If we instead use the delete-then-insert notation, we can represent this a little more cleanly as $e_i(t_j) \circ E_{i-1,j-1} \circ e_d,$ but if the last two characters are the same then this still isn’t quite right. Oh well.

We choose whichever possibility corresponds to the minimal cost in the equation for $D_{i,j}$, breaking ties arbitrarily. Just as we calculated a minimum cost for each entry in the table illustrated in Figure 1, we also calculate a sequence of edits for each entry. The desired sequence corresponds to the entry in the bottom-right of the table.